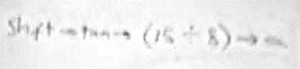Scenario: Lucy teaching trigonometric ratios
Country: UK
Grade (student age): Year 10 (age 14-15)
Contributed by: Anne Thwaites, University of Cambridge, UK
Context – national, curricular, professional, other
The National Curriculum for mathematics in England introduces trigonometric relationships in Key Stage 4 (years 10 and 11, pupil age 14-16). Lucy was reviewing the idea of a trigonometric ratio with her class, before moving on to discuss how to calculate the size of an angle given the lengths of two sides. Lucy was a graduate pre-service teacher, and the lesson took place in a school-based placement towards the end of her one-year teacher preparation.
Scenario
Lucy, a graduate student-teacher, was teaching in an open-entry school (pupil age 11-18) in a small town in the UK. The school divides each year into mathematics groups (by ability) and Lucy was teaching one of the two parallel top groups. This was the final lesson of a series of three in which she had introduced the idea of trigonometric ratios with a Year 10 (pupil age 14-15) class. A box of calculators (or various types) was available in the classroom.
There was an interactive whiteboard and another whiteboard to the side. Lucy used the side-board to write on during the lesson and the 
interactive board for a series of pre-prepared powerpoint slides; she didn’t use the interactive board for any recording. On the first of the powerpoint slides, Lucy had a right-angled triangle (8-15-17) which she used as an example to ask the pupils which ratio gave the tangent of a marked angle.
Having handed out a variety of calculators (some used different protocols/order of operations from others), she revised the procedure to find the tangent of an angle before moving on to find the angle itself. .She said to the class:
“Now, on your calculator, there is a button that looks like this. [draws tan-1 on the side-board] If you press that button and then fifteen divided by eight [tan-1, 15, ¸, 8], you should get the angle.”
When the pupils tried this, they found a variety of angles. Lucy explained that:
“… we want to know what theta is, we want to undo this tan function to find out what angle we have, this button here is the inverse of tan [points to tan-1 written on the side-board], it undoes the tan part so we can find out what angle we would put into tan to get 15 divided by 8.”.
Lucy goes on to describe the possible key presses, using a calculator herself, and says:
“If you do the inverse of tan, which is this button here [again points to tan-1 written on board] - you normally have to press shift, or second function on the calculator to get that [tan-1 ] - then you have 15 divided by 8 and you should get 61.9 degrees. So it might be a different sequence of buttons on each of your calculators but have a play around and see if you can get 61.9o.” As the students started to use their calculators, Lucy suggested that they might need to use brackets and she wrote a possible key sequence on the side-board (see figure below).
Shift ® tan ® ( 15 ¸ 8 ) ® =
During the course of subsequent discussion, she used the term ‘undo’ again, described this as the ‘inverse’ and gave them the analogy “What multiplying is to dividing.” Finally in this section of the lesson and using the same triangle (8, 15, 17), she asked them to find the angle again, but using the cos-1 function, saying “using the inverse function of cos to find this angle” and that they “should get the same answer.”
In this cycle of our research, we interviewed the student-teacher after the lesson. During this meeting we viewed episodes from the video of the lesson and one member of the team led a discussion with the student-teacher in the spirit of stimulated-recall. This discussion was audio recorded and included the following:
Researcher … you’d used inverse very precisely, and indeed at some point talked about inverse function...then at some point used I think the analogy with multiplication ... and division. Was that something that sort of popped into your head, or...?
Lucy Yes it was, actually. … So I explained it with ... inverse function and with multiplication and division. And also we’ve been doing... rearranging formulae a few weeks before...
Researcher Oh, right.
Lucy ... so I was hoping that would kind of click with something we’d done earlier.
Researcher So that they had been using inverse functions at that point?
Lucy Yes, they had.
Knowledge Quartet Coding Commentary
Contributed by: Anne Thwaites, University of Cambridge, UK
Knowledge Quartet Dimension: Connection
Knowledge Quartet Code: Making connections between procedures
Scenario: Lucy teaching trigonometric ratios
In introducing the idea of finding the size of an angle from the lengths of two sides of a right-angled triangle, Lucy uses an inverse function on a calculator. Having told the pupils that they are to use the tan-1 button, she spends some moments explaining that this ‘undoes’ the tan function and linking it to ‘inverse’. At one point she uses multiplication and division as another example of functions which are inverses of each other; there are difficulties with this as we will discuss below but it is evident from the interview that she was deliberately trying to make connections.
So in this section of her lesson, Lucy made connections both to the fact that the pupils are using an inverse function but also linking it to inverse functions with which they are familiar. There is a problem because multiplication (and division) are not ‘complete’ functions; it is necessary to multiply by something (multiply by 3, for example) whereas invtan (tan-1) is a complete function. With hindsight, we might suggest that squaring and its inverse, square rooting, could be a better analogy. Looking to the students’ future learning, it is also worth noting that multiplication and division are one-one relationships whereas the trig functions only possess this relationship in limited ranges – for example, as here, 0-90 degrees.
However this type of linking seems to be an important factor in helping pupils to build their own connections within and between different areas of work in mathematics. Here we saw some of these links being explicitly discussed during the lesson. Then, in the interview with Lucy, we learnt that she was making some of these connections to earlier work.
Multiplication and division, rearranging of formulae (to make different variables the ‘subject’) and solving triangles using trigonometry could be perceived as disparate topics. The notion of doing and undoing, function and inverse, is one of the ‘big ideas’ of mathematics. The Williams report highlights this:
‘Mathematics has a broadly hierarchical structure, but not necessarily (in fact rarely) a linear one. The challenge in planning learning for children is to provide the interlinked ‘bigger picture’ as well as the detail to enable children to recognise how their learning fits together rather than appearing to be piecemeal.’ (Paragraph 239)
Seen from this perspective, Lucy is able to draw these seemingly disparate ideas, and separate topics, into a connected, albeit not perfect, whole. This is a case of making connections across lessons, as opposed to within one lesson.
References
DCFS (2008) Independent Review of Mathematics Teaching in Early Years Settings and Primary Schools (The Williams Report) Department for Children, Schools and Families Publications: Nottingham