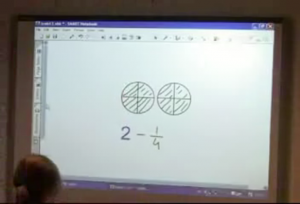Scenario: Hans teaching fractions greater than one
Country: Norway
Grade (student age): Year 5 (age 11-12)
Contributed by: Bodil Kleve, Oslo and Akershus University College of Applied Sciences
Context – national, curricular, professional, other
In our present curriculum LK 06, competence aims for the subject are presented after year 2, year 4, year 7 and year 10. This lesson is from year five. With regard to fractions, competence aims after year 4 do not include any. After year 7 fractions are included in Competence aims for numbers and algebra: “The aim for the education is that the pupil shall be able to
- describe the place value system for decimal numbers, calculate with positive and negative whole numbers, decimal numbers, fractions and percentages, and place them on the real number line
- find common denominators and carry out addition, subtraction and multiplication of fractions”
In grades 5-7 (age 11-13) in Norway, it is quite common when introducing work with fractions to emphasise fractions as part of a whole. Also in most textbooks used in primary schools in Norway, fractions are introduced and emphasised as part of a whole. This was the case for the book used in the class where the research referred to took place.
Scenario
The lesson objective, “to calculate with fractions greater than one” was written on the board. Hans, the teacher, was a young man who had finished his teacher education (specialised in mathematics) 4-5 years ago. He had prepared several exercises for this lesson. A smart board was used and the exercises were (partly) pre written on the smart board. The teacher introduced the exercises and one pupil from class was taken to the board to work out each exercise.
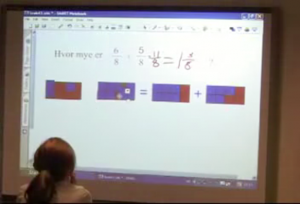
1 The first exercise was to add two fractions, 6/8 + 5/8. Both fractions were illustrated with rectangles, each divided into 8 pieces and with 6 and 5 pieces shaded. Similar illustrations were presented on both sides of an equal sign (see fig 1a).
Fig 1a Numbers and rectangles to illustrate
The left side of the equal sign was used to illustrate how one rectangle (the second) could be filled up (one whole) and three left in the first (see fig 1b)
Fig 1b One rectangle was filled up, and three pieces remained in the other.
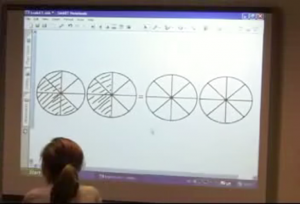
2 In the next exercise, only illustrations of fractions were used to begin with. Hans shaded 5/8 of one circle and 4/8 of another circle (see fig 2a). The pupils were asked to write the fractions with numbers.
Fig 2a
Also here, the circles on one side (this time on the right side of the equal sign) were used to illustrate one whole and 1/8 (See fig 2b)
Fig 2b
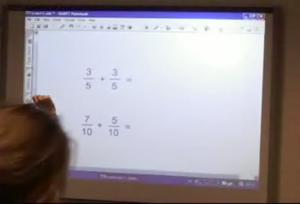
3 Hans: Let us try without illustrations
Now he presented two exercises without illustrations, 3/5 + 3/5 and 7/10 + 7/10, (fig 3). And they were worked out on the board by pupils.
Fig 3
4 Illustration and numbers. Subtracting a fraction from a whole number
The last exercise in this lesson to be worked out in class was 2-1/4, with illustration and is presented below (fig 4)
Fig 4
Knowledge Quartet Coding Commentary
Contributed by: Bodil Kleve, Oslo and Akershus University College of Applied Sciences
Knowledge Quartet Dimension: Connection
Knowledge Quartet Code: Decisions about sequencing (DS)
Scenario: Hans teaching fractions greater than one
Connection as a dimension in the Knowledge Quartet is “concerned with the decisions about sequencing and connectivity” (Rowland, Turner, Thwaites, & Huckstep, 2009, p. 36). One of the codes within this dimension is to “introduce ideas and strategies in an appropriately progressive order” (ibid, p. 37). I suggest that in the scenario described above, the sequence of the exercises was consciously done by the teachers. If the exercises chosen were appropriate for developing a solid concept of improper fractions may be discussed. In all exercises the fractions were presented as part of a whole. According to research, fractions as part of a whole is inconsistent with the existence of improper fractions and possibilities for obtaining a well-developed concept of fractions are limited if one focuses on fractions as part of a whole (Anghileri, 2000; Askew, 2000; Dickson, Brown, & Gibson, 1984).
For this lesson Hans had prepared 4 different exercises to be done in whole class before the pupils were told to work individually with tasks from the textbook. The lesson objective was to learn to calculate with improper fractions. Placing this lesson in the Connection dimension of the KQ and coding it as Decision about Sequencing is based on the progression of the exercises discussed below.
The first exercise is presented with both illustrations and numbers. To work out this exercise they calculated with numbers, converted improper fraction to mixed number which was illustrated on the figure by pulling shaded pieces from one rectangle to fill up the other on the smart board. In this exercise it was possible to get the right answer 1 3/8 by counting shaded pieces on the illustration.
The second exercise was presented without numbers. The pupils were asked about have big part of the first was shaded and then of the second before they worked out the answer. This answer 9/8 was converted to 1 1/8 which was illustrated on the figure (fig 2b). This time, it was not possible to pull the pieces. The teacher erased from one circle and filled up the other.
When starting the third exercise, the teacher said “let us try without illustrations”. This suggests that he consciously wanted the pupils to calculate the sum of two fractions which added up to an improper fraction, without having illustrations as mediating tool.
The fourth exercise was different from the three first in several ways. It was illustrated with circles and numbers to be calculated was written below. This time the illustrations were not on two sides of an equal sign, it was subtraction, and it started with a whole number. The exercise for the pupils was both to illustrate how much to erase from the figure and also to work it out with numbers.
Hans’ choices of illustrations and numbers / only illustrations / only numbers reflected a progression in the lesson. However, the fourth exercise required a subtraction and thus introduced an added complexity. In this example subtraction was thought of as “take away”, but could also be comparison. Thus there was a leap here, or a missing link. It might have been preferable here to have an exercise that was adding, with one of the numbers as a mixed number and the other as a fraction.
Focusing on fractions as part of a whole suggests a limitation of Hans’ foundational knowledge. He could usefully have used a number line marked in eights for the first example. Hans could usefully attend to the Foundation dimension which incorporates knowledge about common errors and misconceptions, and also research about what factors have proved to be significant with regard to pupils’ understanding (or lack of it) of improper fractions (Kleve, 2010). Also, that there was a leap from working with proper fractions and addition to subtraction which incorporated whole number, fraction and a mixed number (the answer), indicated a limitation in his decision of the sequencing of exercises.
References
Anghileri, J. (2000). Teaching number sense. London: Continuum.
Askew, M. (2000). What does it mean to learn? What is effective teaching? In J. Anghileri (Ed.), Principles and Practices in Arithmetic teaching (pp. 134-146). Buckingham Open University Press.
Dickson, L., Brown, M., & Gibson, O. (1984). Children learning mathematics: A teacher's guide to recent research: The Alden Press Ltd, Oxford.
Kleve, B. (2010). Contingent Moments in a lesson on fractions. [Current Report]. Research in Mathematics Education, 12(2), 157-158.
Rowland, T., Turner, F., Thwaites, A., & Huckstep, P. (2009). Developing Primary Mathematics Teaching, Reflecting on Practice with the Knowledge Quartet. London: SAGE publications Ltd.