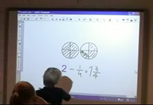Scenario: Hans teaching fractions greater than one
Country: Norway
Grade (student age): Year 5 (age 11-12)
Contributed by: Bodil Kleve, Oslo and Akershus University College of Applied Sciences
Context – national, curricular, professional, other
In our present curriculum LK 06, competence aims for the subject are presented after year 2, year 4, year 7 and year 10. This lesson is from year five. With regard to fractions, competence aims after year 4 do not include any. After year 7 fractions are included in Competence aims for numbers and algebra: “The aim for the education is that the pupil shall be able to
- describe the place value system for decimal numbers, calculate with positive and negative whole numbers, decimal numbers, fractions and percentages, and place them on the real number line
- find common denominators and carry out addition, subtraction and multiplication of fractions”
In grades 5-7 (age 11-13) in Norway, it is quite common when introducing work with fractions to emphasise fractions as part of a whole. Also in most textbooks used in primary schools in Norway, fractions are introduced and emphasised as part of a whole. This was the case for the book used in the class where the research referred to took place.
Scenario
The lesson objective was written on the smart board: ‘To be able to calculate with fractions which are bigger than one whole’. The episode referred to here, took place about 15 minutes out in the lesson. Several tasks with improper fractions illustrated with rectangles or circles had taken place earlier in the lesson. The task here was to take away ¼ from 2. Hans, the teacher, was a young man who had finished his teacher education (specialised in mathematics) 4-5 years ago. He had drawn 2 circles on the smart board, each circle divided into quarters which were shaded, and he wrote 2-1/4 under the circles (see below). He addressed the class:
Hans: Okay, what about two minus one fourth? Espen
Espen went to the board
Espen: It makes two minus one fourth. Those two are two. Then I just erase these.
Espen erased two ¼ pieces of the second circle (see below)
A boy in class (Marius) then called out:
Marius: Now you are erasing one half!
Hans: To Espen: Are you sure?
Marius: Called out: Not one fourth of two, not one fourth of two, not one fourth of two
Hans: To Marius: Hush. I asked Espen to show on the drawing, so he is doing right. To Espen:
But should you have taken, ehm, how much have you actually taken away?
Espen: If that is two so half of that
Hans: But what is the whole, Espen?
Espen: Can take this, two is the same as four fourth (wrote 4/4 on the board)
Hans: Is it?
Marius: (called out): four fourth, that is one!
Hans: To Marius: Let him finish thinking
Espen now shaded one of the two pieces he had erased earlier and wrote 1 ¾ on the board (see below)
Hans: That is correct. But I wondered, I am very curious to know how did you come to, … for what is the whole actually?
Even: Because I counted that as one. I looked upon it as two twoth and not as two wholes
After this, the lesson carried on and Hans did not discuss or mention Espen’s conception of what the whole was. The rest of the class (including Marius) was not invited to discuss Espen’s solution of the task.
Knowledge Quartet Coding Commentary
Contributed by: Bodil Kleve, Oslo and Akershus University College of Applied Sciences
Knowledge Quartet Dimension: Contingency
Knowledge Quartet Code: Responding to Children’s ideas (RCI)
Scenario: Hans teaching fractions greater than one
In this episode, one of the according to the teacher Hans, “brightest” pupils in the class, Espen, was taken to the board to work out 2 – ¼ illustrated by two circles.
Surprisingly, Espen erased two ¼ pieces. According to what Hans said in a conversation after this lesson, he had not anticipated this, so he had to “think on his feet”. Hans responded to the unexpected (Rowland, Turner, Thwaites, & Huckstep, 2009). A mismatch between Hans’ intention with the task and Espen’s conception of it occurred. While Hans looked upon one circle as “the whole”, Espen saw the two circles as the whole and erased one fourth of two which is one half.
In this instance, Hans could have reacted in several ways. First, he could have chosen to rephrase Marius’ input “not one fourth of two” and leave it there. Second, he could have told Espen, that he meant one fourth of one circle, and leave it there. Hans could also have taken the illustrations away and asked Espen to solve the task 2-1/4 without use of circles as illustrations. Instead, (considering Espen to be a bright pupil), Hans chose to challenge Espen’s thinking “But I wondered, I am very curious to know how did you come to..”. Although Espen’s answer was unexpected, Hans chose to challenge his thinking, and in that respect he dealt appropriately with Espen’s response. However, Hans never acknowledged Espen’s conception of the task and in that respect the appropriateness of Hans’ response may be questioned. And the two different conceptions of what was the whole, one circle or both circles were never discussed. In this respect, Hans’ foundational knowledge seemed to be weak. One question is if Espen did wrong. According to Hans, Espen did wrong. According to the task 2 – ¼ Espen did wrong. But looking at the illustration and taking away one fourth of the two circles, Espen was right.
However, in challenging Espen’s thinking, Hans constrained Espen’s answer by adding: “for what is the whole, actually?”. This addition indicated that Espen’s conception of “the whole” was not correct. This is underpinned when Espen realised that Hans had another conception of “the whole” and Espen gave up his conception (the whole consists of two circles) by re-shading one of the quarters and Hans evaluated this as “correct”.
This episode exemplifies difficulties which can occur when focus on fractions as part of a whole (which makes sense in work with fractions smaller than one) is transferred to improper fractions. Research suggests that focus on fraction as part of a whole can prevent children in developing a solid fraction concept (Anghileri, 2000; Askew, 2000). And focusing on fraction as part of a whole is inconsistent with the existence of improper fractions (Dickson, Gibson, & Brown, 1984; Rowland, et al., 2009
References
Anghileri, J. (2000). Teaching number sense. London: Continuum.
Askew, M. (2000). What does it mean to learn? What is effective teaching? In J. Anghileri (Ed.), Principles and Practices in Arithmetic teaching (pp. 134-146). Buckingham Open University Press.
Dickson, L., Gibson, O., & Brown, M. (1984). Children learning mathematics : a teacher's guide to recent research. Eastbourne, East Sussex: Holt, Rinehart and Wilson.
Rowland, T., Turner, F., Thwaites, A., & Huckstep, P. (2009). Developing Primary Mathematics Teaching, Reflecting on Practice with the Knowledge Quartet. London: SAGE publications Ltd.