Scenario: Solving problems using Schema-Based Instruction
Country: Cyprus
Grade (student age): Year 5 (age 10-11)
Contributed by: Marilena Petrou
Context – national, curricular, professional, other
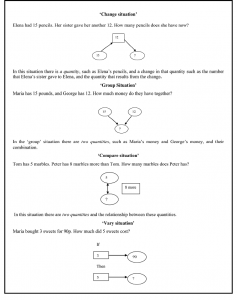
Schema-Based Instruction aims to develop students’ understanding of the basic relations found in arithmetic word problems (Marshall, 1995). Students are taught to map features of word problems onto problem schemata. Figure 1 illustrates the four schemas that are included in mathematics textbooks in Cyprus used to describe the semantic relations found in story problems, namely, ‘change’, ‘group’, ‘compare’, and ‘vary’
Figure 1: Schema- problems
The scenario described below comes from a lesson taught by Elsa. Elsa, a final year university student in a teacher preparation programme, was teching problem solving using Schema-Based Instruction with a Year 5 (pupils age 10-11) class. The lesson took place in a school-based placement towards the end of her four-year teacher preparation. Figure 2
Scenario
Figure 2 illustrates one of the activities that she used in her lesson. In this activity the students were given the diagram presented in Figure 2 and asked to develop their own problems. Some of the problems proposed are also presented in Figure 2. The diagram shown in Figure 2 describes a ‘change’ situation and it could give rise to addition and subtraction.
Figure 2. Problems suggested by students
The problems suggested by the students in Figure 2 were all accepted as correct by the teacher. Students suggestion were not discuss in the class.
Knowledge Quartet Coding Commentary
Contributed by: Marilena Petrou
Knowledge Quartet Dimension: Contingency
Knowledge Quartet Code: Responding to children’s ideas (RCI)
Scenario: Elsa teaching problem solving using schema-based instruction
Notice that among the student suggested problems only the first one is correct. For example, in
problem 2 the information in the rectangle should be, , since he sold of .
In problem 3, of coffee does not make any sense. Problem 4 is incorrect and does not represent a
change situation. However, Elsa accepted all the problems as being correct without exploring the students’ proposals or probing the ways in which they were making sense of the diagram. It seems that she did not recognise that students’ suggestions need conceptual foundation. Her unwillingness to discuss students’ responses could be attributed to her own limited understanding. In addition, the fact that she did not discuss students’ suggestions prevented other students from noticing the mistake. Furthermore, the last problem represented a group situation. Elsa seems to be unaware of the mathematical significance, for the whole class, of discussing this suggestion. This episode offered her a good opportunity to make an explicit link between a group and a change situation, but she did not take advantage of it.
References
Marshall, S.D. (1995) Schemas in problem solving, (Cambridge, Cambridge University Press).