Scenario: Heidi revising percentages
Country: UK
Grade (student age): Year 8 (age 12-13)
Contributed by: Anne Thwaites, University of Cambridge, UK
Context – national, curricular, professional, other
The National Curriculum for mathematics in England includes work on fractions, decimals and percentages in Key Stage 3 (years 7-9, pupil age 11-14). Heidi was revising the four operations with fractions, before moving on to discuss some word problems related to percentages. Having completed a mathematics degree, which included an optional mathematics education element, Heidi was a graduate on a pre-service training course. The lesson took place in a school-based placement towards the end of her one-year teacher preparation.
Scenario
Heidi, a graduate student-teacher, was teaching in an open entry secondary school (pupil age 11-18) in a village in the UK. The school divides each year into mathematics groups (by ability) and Heidi was teaching one of the two parallel top groups in Year 8 (pupil age 12-13). This was a revision lesson in which she is considering fractions and percentages with the class.
 Heidi had an initial, whole class activity of completing a 3x3 fraction magic square –the sums of each column, row and diagonal gave the same result. To start, the square had a layout which Heidi had written on the interactive whiteboard (IWB) as shown in the figure.
Heidi had an initial, whole class activity of completing a 3x3 fraction magic square –the sums of each column, row and diagonal gave the same result. To start, the square had a layout which Heidi had written on the interactive whiteboard (IWB) as shown in the figure.
Heidi checked with the class that they remembered the ‘rule’ for a magic square and then asked how they might solve this particular example. One pupil suggested that they added the fractions in the left hand column (1⁄2, 1 2/3, 5/6), Heidi asked how they will add them and he said they needed to find the ‘common denominator’, Heidi repeated the term ‘common denominator’. She then said, “There is something I might want to do first, actually.” A second pupil suggested changing them into ‘improper fractions’ and said that 1 2/3 will become 5/3.
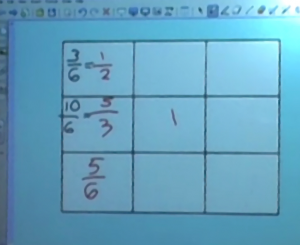 Having agreed that the common denominator is 6, Heidi added 10/6 to the cell with and to the cell with 5/3 and 3/6 (equivalent fractions, although neither Heidi nor the children use this term). She recorded these alternatives on the IWB.
Having agreed that the common denominator is 6, Heidi added 10/6 to the cell with and to the cell with 5/3 and 3/6 (equivalent fractions, although neither Heidi nor the children use this term). She recorded these alternatives on the IWB.
They continued to find the total for the column -18/6 or 3 and then to work through to the solution, finding improper and equivalent fractions for most of the cells. Typically, when wanting to record a fraction in its equivalent forms, Heidi asked the class “How else could I write that to help adding up?” She didn’t use the term ‘equivalent fraction’ but did write them as equal to each other.
In the next section of the lesson, working on percentage problems, the pupils used the terms ‘divide’, ‘times’, ‘add’ and ‘take away’ for the four number operations. Heidi echoed this language and recorded the operations in symbolic form on the IWB. For example, for the calculation 130/100 × 5 one pupil said “a hundred and thirty divided by a hundred timesed by 5” which Heidi reiterated.
In this cycle of our research, we were interviewing the student-teacher after the lesson. During this meeting we viewed episodes from the video of the lesson and one member of the team led a discussion with the student-teacher in the spirit of stimulated-recall. This discussion was audio recorded and included the following:
Researcher … what are your views about mathematical language... and notations and...?
Heidi … I would always consider timesing … to be multiplying. I think I’ve grown up around saying timesing and take away ... I kind of repeat what they say sometimes, if they say, ‘Times this by five,’ I’ll say, ‘Yeah, okay, so we times it by five.’ And … provided everybody in the class is aware of what timesing and take away means I wouldn't have any problem with them saying it. And I would say it myself I suppose quite a lot.
Researcher … take away particularly is quite interesting because it’s one model of subtraction. And, in fact, looking at differences, you can do it by adding on. … And therefore, it’s not take away at all. ... do you think that that matters ...?
Heidi … I’ve never thought about the connotations of, ‘actually, you’re adding on.’ ... I’ve never thought of that being linked to the term take away. I’ve always considered take away to be just a synonym for, em, subtract, just like plus is a synonym for add.
…
Researcher But do you have a picture in your head if you’re going to do a calculation like that?
Heidi Em, no. If you said the question to me out loud, regardless of whether you said take away or subtract I would just see a straight line. I would see the sum and write it out in my head...
Researcher And then how would you work it out?
Heidi ... add on. Well, actually, sometimes I don’t, I think it depends on the numbers.
Further into the interview, Heidi discussed division and the two symbols for the operation:
Heidi ... But the interesting thing for me with divide … is there’s almost two symbols for divide, there’s, you know, the fraction line... or the actual symbol. … it’s more useful, I feel, to put it over another number and introduce that earlier because then it starts linking with fractions. And I found a lot of pupils don't get that link at all; they have no idea that a quarter is one divided by four, and they’ve never seen that. And I try and show them that as much as possible, because even though there’s only one word, there is a lot of different ways you can show divide.
Knowledge Quartet Coding Commentary
Contributed by: Anne Thwaites, University of Cambridge, UK
Knowledge Quartet Dimension: Foundation
Knowledge Quartet Code: Use of terminology
Scenario: Heidi revising percentages
In working through the fraction magic square with the class, Heidi responds to the pupils’ use of the terms ‘common denominator’ and ‘improper fraction’ by incorporating them into her own commentary of what they are doing. This is language which has a precise meaning within mathematics. Although they make use of equivalent fractions throughout this section of the lesson, neither she nor any of the children use the term. So here we have a marked contrast, on one hand Heidi is using this precise language to express some of the processes that they are doing – finding common denominators, expressing fractions in their improper form – but then she does not take the opportunity to use the term ‘equivalent fraction’ when she is finding the equivalents. As we shall see below, she wants to use the language that the pupils offer but it may be that she misses an opportunity here to develop their mathematical language to include mathematical terms which encapsulate important mathematical ideas.
As we have seen both from the lesson extracts and in the interview, Heidi is very ready to accept the language that the pupils use – later in this lesson (and in another that we observed) she repeats their use of ‘times’ or ‘timesing’ and ‘take away’ in talking about multiplication and subtraction. We are interested by Heidi’s apparent reluctance to use the terms ‘multiply’ and ‘subtract’ and wonder whether her preferred use of the terms that the pupils are suggesting may reinforce one particular model for the operation. This may not be most beneficial for the pupils in the longer term and she acknowledges that the numbers in any given example may dictate which model she may prefer. It may also suggest that she has not had the opportunity to recognise these different models, since she may well use them instinctively, and is one of those people who has not experienced difficulties with mathematics.
In the interview, Heidi discusses division and here her experience has caused her to favour one form of representation of the symbol for division over another, in order to build links with other ideas. Indeed she is building her experience from one year group and class to another as she says:
“… they have no idea that a quarter is one divided by four, and they’ve never seen that. And I try and show them that as much as possible, because even though there’s only one word, there is a lot of different ways you can show divide.”
So an awareness of the relationship between terminology, symbols and related concepts or processes can help to build the network of links between different areas of mathematics; in this case Heidi is developing some of these but may be missing some opportunities as well.
In terms of Heidi’s mathematical knowledge for teaching, she already has an understanding of the pedagogical need to use correct mathematical terminology. However, there are gaps in her knowledge of what different terms mean; for example, she thinks that ‘take away’ is synonymous with subtraction, when in fact take away is one structure for subtraction.
