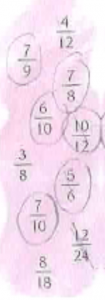
Scenario: Find all fractions larger than 1/2
Country: Norway
Grade (student age): Year 6 (age 11-12)
Contributed by: Ove Gunnar Drageset, University of Tromsoe, Norway
Context
The teacher has 20 years of teaching experience. The lesson is at grade 6 well into the second half of the year. The competence goals in the Norwegian curriculum are not formulated for each year, but are given after the completion of grade 4, 7 and 10. The students have only met fractions like ½ and ¼ used in everyday situations prior to fifth grade. The competence goals regarding fractions after grade seven focuses on calculations using positive and negative fractions, and placing fractions on a number line.
The task is to find all fractions larger than ½ from a pink sky (see figure at the left) containing several fractions. First this happens:
T: Did you find any that are larger than one half?
SE: Yes
T: Tell me one that is larger than one half.
SE: Five six … five sixths.
T: You have found that five sixths is larger than one half (writes 5/6). Why do you know with certainty that this is larger than one half?
SE: Because three … is one half and … (interrupted by the teacher)
09 T: Yes. Because three sixths is one half (writes 3/6=1/2). Right? When we have the half in the numerator of the denominator then we have one half. Then we can find all that have more than the half in the numerator…
The method of dividing the denominator by two to find one half and then comparing the result with the numerator is the teacher’s preferred method. Then a student comes up with another method:
SR: Ehh … at seven and nine … I think in another way. I think in a way that (teacher writes 7/9)… seven … eh … for example seven … eh is seven plus seven that is … that is … eh fourteen, and then it is not fourteen below in the denominator.
T: But you said that seven ninths is larger than one half. Wasn’t that what you said?
SR: Yes
T: Yes. But then you started with fourteenths. How many fourteenths did you find in the pink cloud?
SR: Eeh … no it wasn’t that I answered. If you add seven … if you add seven then … if the denominator had been fourteen then it had been one half. But it is not fourteen, it is nine, it is smaller than fourteen. Then it is more than one half.
T: Okay. Then ... but … SR says that seven ninths is more than one half because she thinks that if she should have one half she had to have seven fourteenths, and nine is smaller than fourteen. You have fewer pieces to divide it into. Mmm.
Knowledge Quartet Coding Commentary
Contributed by: Ove Gunnar Drageset, University of Tromsoe
Knowledge Quartet Dimension: Connection
Knowledge Quartet Code: Responding to children’s ideas (RCI)
Scenario: Find all fractions larger than ½
The student uses a method of doubling the numerator to find the denominator necessary to make a fraction equal to one half, and then comparing the doubled numerator with the existing denominator to decide whether the fractions is smaller or larger than one half. The method suggested by the student has the advantage that it works also with odd numerators without having to use decimals. On the other hand, it might be more difficult to understand.
First, the teacher does not understand the student approach, but after a repeated explanation by the student the teacher understands and recapitulates to explain the rest of the students. But on the next task (not included here) the teacher returns to the preferred method of finding half of the denominator.
The teacher acknowledges the student’s idea after several repeated explanations from the student, but does not incorporate the idea. Instead, the teacher keeps on with her initial method even though it is clearly more limited than the student’s method. It is of course not possible to incorporate all ideas, but in this case there would have been clear advantages both because the student’s method also works with odd numerators and because a discussion of advantages and disadvantages of these two methods could have been fruitful. Because of this, the example is considered to be a negative example of RCI.