Scenario: Laura teaching column multiplication
Country: UK
Grade (student age): Year 5 (age 9-10)
Contributed by: Tim Rowland, University of Cambridge, UK
Context: national, curricular, professional, other
At the time when this lesson was recorded, mathematics in primary schools was prescribed by a National Numeracy Strategy (DfEE, 1999) and a related curriculum framework. The framework suggests progression from mental methods to informal and "expanded" written methods, thence to standard, contracted algorithms. The key focus of this lesson was on teaching column multiplication of whole numbers, specifically multiplying a two-digit number by a single digit number. The intended method is a kind of staging-post between a transparent 'grid' method (see below) and the fully-contracted algorithm.
Laura was a graduate pre-service teacher, and the lesson took place in a school-based placement towards the end of her one-year teacher preparation.
Scenario
Laura reminded the class that they had recently been working on multiplication using the 'grid' method (see below). Simon was invited to the whiteboard to demonstrate the method for 9x37. He wrote:
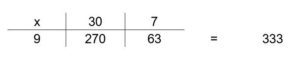
Laura then said that they would be learning "another way". She proceeded to write the calculation for 9x37 on the whiteboard in a conventional but elaborated column format, explaining as she went along:
Laura performed the sum 270+63 by column addition from the right, "carrying" the 1 (from 7+6=13) from the tens into the hundreds column. She wrote the headings h, t, u (i.e. hundreds, tens, units, as shown) above the three columns.
Next, Laura showed how to "set out" 49x8 in the new format, then the first question (19x4) of the exercises to follow. This was followed by seatwork on exercises that Laura had displayed on the wall.
In a concluding eight-minute plenary, Laura asked one boy, Sean, to demonstrate the new method with the example 27x9. Sean got into difficulty; he wrote 27 and x9 in the first two rows as expected, but then wrote 20x7 and 2x9 (instead of 20x9 and 7x9) to the left in the rows below.
Knowledge Quartet Coding Commentary
Contributed by: Tim Rowland, University of Cambridge, UK
Knowledge Quartet Dimension: Transformation
Knowledge Quartet Code: Teacher demonstration (of a procedure)
Scenario: Laura teaching column multiplication
Laura's intention was that she would demonstrate to the class how to carry out this new written multiplication procedure, and that they, in turn, would mimic her demonstration to perform the exercise examples by an analogous procedure.
Laura did indeed perform three such calculations on the whiteboard, and it is reasonable to expect that she succeeded in her aim (for the children to learn and imitate it) to some extent, though we do see evidence to suggest that Sean had not perceived the structure of this new algorithm.
It is possible to identify ways in which Laura could reflect on her demonstration with a view to improving it. In particular, the close connection between the 'expanded-column' layout that she teaches them and the grid method with which they are familiar is not exploited, and so the column approach looks like an entirely different method rather than a fairly natural development from the grid. Indeed, if the grid were stood on its side, it would match the new algorithm to a significant extent.
Furthermore, the rationale for her choice of examples is not clear, especially those that follow the initial demonstration. The product 49x8 would be more efficiently (and more meaningfully) carried out by a mental method, with compensation from 50x8, and this would reflect a more thoughtful selection of calculation strategy. A similar point might be made about 19x4.
A more extended account and analysis of this lesson is given in Rowland, Huckstep and Turner (2005), and also in a paper (Turner and Rowland, 2007; downloadable from a link at http://www.maths-ed.org.uk/mkit/seminar5.html We consider this to be a good example of 'Teacher demonstration of a procedure' because Laura emphases procedural features of the column algorithm, such as how to "set it out" with little apparent concern for conceptual understanding.
References
DfEE (1999) The National Numeracy Strategy: framework for teaching mathematics from Reception to Year 6. Sudbury: DfEE Publications.
Rowland, T., Huckstep, P. and Thwaites, A. (2005) Developing mathematics teaching: the genesis of the Knowledge Quartet. Scientia Pedagogica Experimentalis XLII(2), pp. 331-350.